21天学会SICP

序言 #

SICP = Structure and Interpretation of Computer Programs

关键词：结构、解释、计算机程序

是一本主要讲述计算机程序的书，内部包含大量的练习题，如果严谨的都学完，需要比较大的精力。

说实话，我当年大学课程如果有这个就好了
说实话的实话，如果当年有这门课，估计我也在打盹

项目	说明
	mit在线课程这门课，在mit有公开课程，来自2005上课的录像
	豆瓣地址
作者：Harold Abelson ，1947年出生，是mit的计算机教授2007年的照片	wikipedia mit的主页
在这里继续推荐一个其他老师：这是yinwang的授业恩师Daniel P FriedmanIndiana University的计算机教授这张照片比较年轻了	Daniel P Friedman

观点 #

这本书中的内容，不仅仅是编程，作者花了很多篇幅在讲解算法上。这些算法主要是类似泰勒展开等适用于计算机的改造。

我本人只细致的看到了第一章，因此，这次也是梗概介绍。无法深入到细节中。

SICP在讲些什么 #

第一章：构造抽象过程 #

1.1 程序的基础 #

Lisp语言介绍 #

lisp是20世纪50年代后期发明的一种语言，主要是为了对 list 进行 processing的语言。称为【递归方程】，作者是John McCarthy¹ Lisp的名字，来自表处理（LISt PROCESSING），Lisp语言的设计是提供了符号计算的能力，去解决一些程序设计问题比如代数表达式的符号微分和积分。

Lisp不是刻意设计的结果，是一种实验性的，非正式的发展实现。lisp发展到现在，已经有很多种方言了，参见下面的发展图

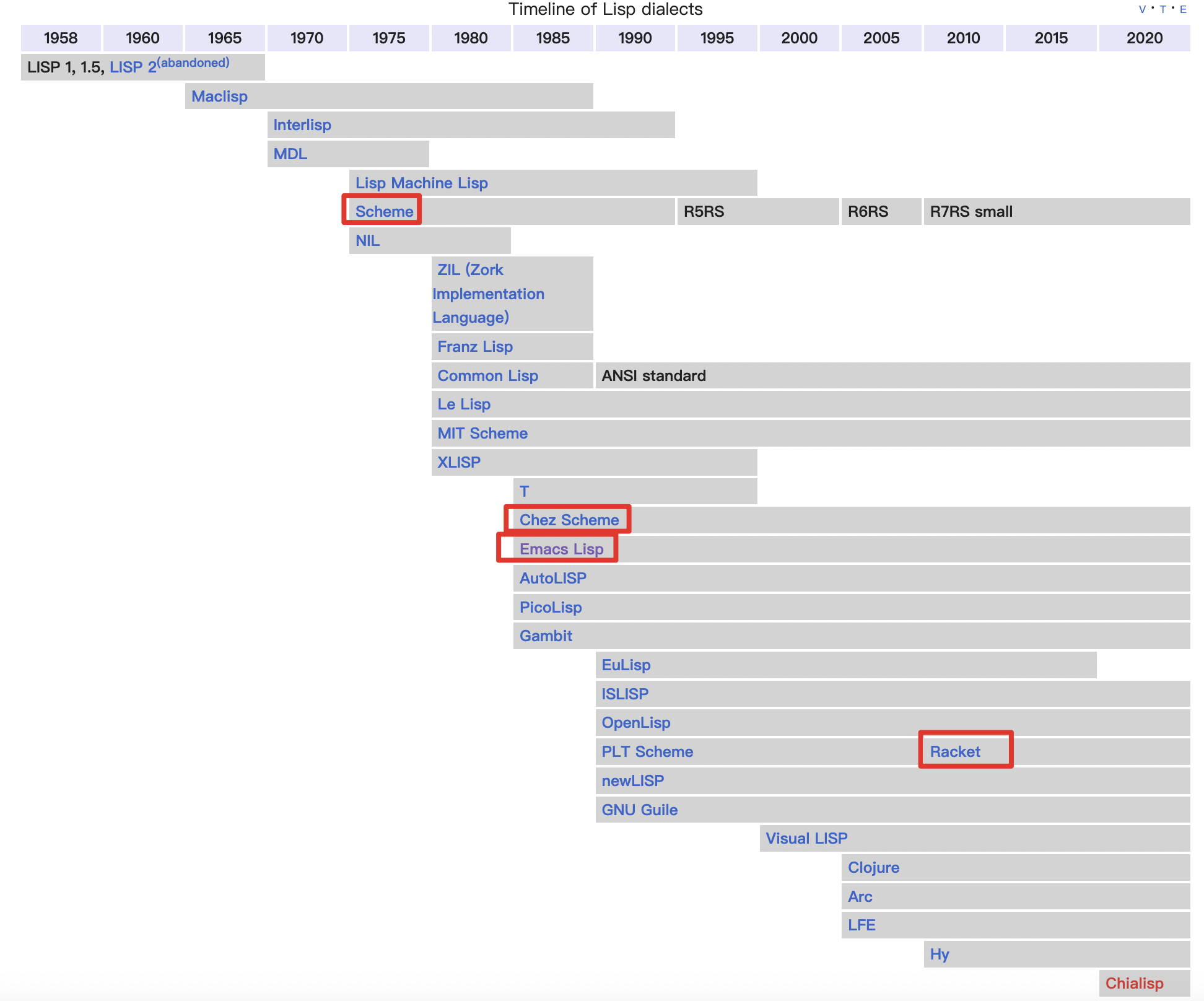
值得一说的是，ChezScheme[fn:4]是业界最快的scheme编译器，之前是在思科的收费软件，后来进行了开源

lisp 主要的特点，在于将『数据』和『程序』进行了几乎无差别的对待，在数据处理方面，效果更好。

提供2个最简单的lisp代码开发环境 #

racket，封装了很多功能，非常不错，就是IDE有点搓搓的
emacs-lisp，这是emacs自带的开发语言，也是一种scheme方言，格式和书里面的不太相同，但是大同小异，安装了emacs就直接能用，但是学习成本有点高。

1.2 过程和计算 #

抽象编程基础，递归 vs 迭代 #

举例：这是lisp中的一个函数，求斐波那契数列的，用的是一个递归

(define (fib n)
   (cond ((= n 0) 0)
         ((= n 1) 1)
         (else (+ (fib (- n 1))
                  (fib (- n 2))))))

下面是fib的迭代实现，即，将树形递归变成尾递归，执行效率有了本质的提升。

(define (fib n) (fib-iter 1 0 n))
(define (fib-iter a b count)
     (if (= count 0)
      b
     (fib-iter (+ a b) a (- count 1))))

进一步，如果仔细思考，会发现，这个迭代实现，其实就是动态规划的雏形。

【真AI】理解程序：代换模型 #

(define (++ a b)
     (if ( = a 0)
         b
         (inc (++ (dec a) b)))
 )

;; (++ 4 5)
;; (inc (++ 3 5)))
;; (inc (inc (++ 2 5)))
;; (inc (inc (inc (++ 1 5))))
;; (inc (inc (inc (inc (++ 0 5)))))
;; (inc (inc (inc (inc (5)))))
;; (inc (inc (inc (6))))
;; (inc (inc 7))
;; (inc 8)
;; 9

代换模型的举例，就是将程序运行的每个步骤，用笔写出来，这样有助于理解程序

(define (+ a b)
   (if ( = a 0)
   b
   (+ (dec a) (inc b))))

;;(++ 4 5)
;;(++ 3 6)
;;(++ 2 7)
;;(++ 1 8)
;;(++ 0 9)
;;9

比如同样是一个++ 函数的实现，但是在不同的递归结构中，逻辑完全不一样，占用的空间也完全不同，这样，时间复杂度和空间复杂度都不同。

这其中，作者还针对不同的很多数学问题，使用不同的方案实现，带领大家更充分的体验时间复杂度和空间复杂度。

1.3 高阶函数抽象 #

这一部分，主要表达，可以将函数本身，作为一个函数的入参、出参，这样操作函数的函数，叫做高阶函数。

举例如下：

(define (sum-integers a b) ;; 从a加到b的和 (sum-integers 1 3) = 1 + 2 + 3
   (if (> a b) 
       0 
       (+ a 
          (sum-integers (+ a 1) b))))

(define (sum-cubes a b) ;; 计算从a加到b的立方，比如 (sum-cubes 1 3) 1^3 + 2^3 + 3^3
    (if (> a b) 
        0 
        (+ 
          (cube a) 
          (sum-cubes (+ a 1) b))))

这种模式的函数，其实可以比较精确的表示求和公式，并且可以封装细节

$$ \sum_{n=a}^b{f(n) = f(a) + f(a+1) +...+f(b)} $$

(define (⟨name⟩ a b)
   (if (> a b) 
       0 
       (+ 
        (⟨term⟩ a) 
        (⟨name⟩ (⟨next⟩ a) b))))

抽象的函数实现 #

经过抽象，可以得出上面的范式，这样可以将范式进行重写

(define (sum term a next b)
  (if (> a b) 
       0 
      (+ (term a)
         (sum term (next a) next b))))

最一开始的两个函数就变成了这个

;; 求立方和
(define (inc n) (+ n 1)) 
(define (sum-cubes a b) 
  (sum cube a inc b))

;;单纯求和
(define (identity x) x) 
(define (sum-integers a b) 
   (sum identity a inc b))

匿名函数 #

最外面的函数，作为工具人，存活的时间比较短，这时候，最好用工具函数替代，大名鼎鼎的lambda出现了

$$ lambda,\lambda \\ (lambda\quad (x)\quad (*\quad x\quad x\quad x)) \\ 一个立方函数就定义出来了 $$

(define (sum-cubes a b) 
  (sum (lambda (x) (* x x x)) a inc b))

返回函数的函数 #

这其实是混淆的将函数、value都传递进去了，输出的是value。也有那种输出的是函数的直接实现

(define (sum-fun f)
  (define (sum-fun-f a b)
      (if (> a b)
          0
          (+ (f a)
             (sum-fun-f (+ a 1 ) b))))
  sum-fun-f)

((sum-fun cube) 1 9)

照样可以算出来1-9的立方和

1.255 老张叨叨叨 #

上面的内容只是第一章的九牛之一毛。

给各位开开眼，也给我自己开开眼

大量的练习题 #

第一章总共3个小节，52页书，习题就有46道，这哪里是书，简直是习题集。

然而，我认为这样的方式，比较有学习的效果。一件事想快速上手，练习最重要。

非常丰富的算法 #

我怀疑我大学真是白费了
如果把这些练习题或者算法都弄明白了的话，算是有些心得了

牛顿法求平方根
换零钱方式的统计
帕斯卡三角形的打印（杨辉三角）
斐波纳契数列的常数证明：证明 $ Fib(n) = (\phi^n -\gamma^n)/\sqrt{5}, 其中，\phi = (1 + \sqrt{5})/2,\gamma=(1-\sqrt5)/2$
sin函数的归纳法证明
最大公约数计算
素数检测（费马检查）以及对应的优化过程
$\pi$ 的收敛过程和计算
区间折半寻找方程的根
找函数的不动点（证明黄金分割点是$x->1+1/x$的不动点）
利用欧拉展开式求自然对数 $e$ 的近似值
利用正切函数的连分式求正切函数的近似值
平滑函数、平均阻尼函数
组合函数 double，compose，succ等
最难的是pred函数

第二章：构造数据抽象 #

pair对象及其扩展操作 #

这一章，引入了scheme的数据对象，即：pair，利用这种数据结构，可以做很多事情，

(define pair
 (cons 1 null)
 )
(car pair) ;; 获取第一个元素
(cdr pair) ;; 获取第二个元素
;;;;;
> 1
> '()

;; 
(cons 1 2)
;;> '(1 . 2)
(cons 1 (cons 2 null))
;;> '(1 2)

这种结构，本质上就是链表，每个结构，有2部分，可以存储指针，也可以存储数据

用pair 构建了一个链表

(cons 1 
      (cons 2 
            (cons 3 
                  (cons 4 nil))))
(list 1 2 3 4)
'(1 2 3 4)

注意，这里后两个写法都比较明白，但是前一个写法你会知道，这是一个嵌套的过程，要想拿到4，就必须拿到3，没办法直接拿到4。

在代码里面你会发现，这种结构类似俄罗斯套娃

pair带来的数据结构以及闭包特性（Closure） #

这种结构的优缺点比较明显

数据绑定性，可以在一个变量中，套任意层，不同数据是被严格绑定等，比如用来表示无理数的分子和分母，直角坐标系的角度
不可变更性，所有的排序、筛选、变更运算，都会产生一个新的结构，而非原来的结构
递归优先，结构非常适合递归，如果不是递归，操作起来真的有点费劲
闭包支持：通过cons组合的数据对象，其操作结果本身依然可以通过同样的操作再进行组合。

这种结构本身具有一定的限制，但是又有一定的自由度

纯粹数据结构

嵌套结构

套娃结构（chain）

(cons (list 1 2) (list 3 4))
> '((1 2) 3 4)

一开始可能不太好理解，但是事实就是这样，只有 (1 2) 元素不是套娃中的一部分，(3 4) 是标准的套娃结构，因此，上面的写法，其实和这个一样的

(list (list 1 2) 3 4)

使用pair实现的计算器系统 #

最终，经过各种逻辑抽象，会利用pair 这个结构，编写完成一个支持各种计算的计算器模型，并且根据继承关系，自动判定数据类型，给出计算结果

老张叨叨叨 #

这一章一共有95页，但是有97道练习题。

核心就是pair这个结构，并且围绕这个结构进行学习，然后中间又夹杂了很多很多的算法和公式。我觉得他们肯定是觉得大学生未出茅庐，只有数学是能有直观感受的了。

后续的三章，我个人实在hold不住，干脆介绍下学习sicp的一个示范把

一个俄罗斯小哥的学习记录

Experience-Report-Presentation.pdf

第三章：模块化、对象和状态 #

从这一章开始，必须深入看和敲代码了，浮皮潦草的看一遍，基本上和没看一样

我只是浮皮潦草看了了一下，因此只做一些梗概的说明。

赋值和局部状态： #

通过银行账户的模型，介绍了局部变量 和全局变量的关系，一个函数的入参，就是局部变量，以及在这个函数中定义的所有对象。可见性只在函数中，这个是什么原因

求值的环境（env）模型 #

引入了环境的概念，为了实现上面的局部变脸以及层层递归之间，每个变量的不同value，就需要引入这种环境。对于咱们来讲，相对比较容易理解，就是局部变量表和入栈出栈的关系。比如JVM中的运行时模型

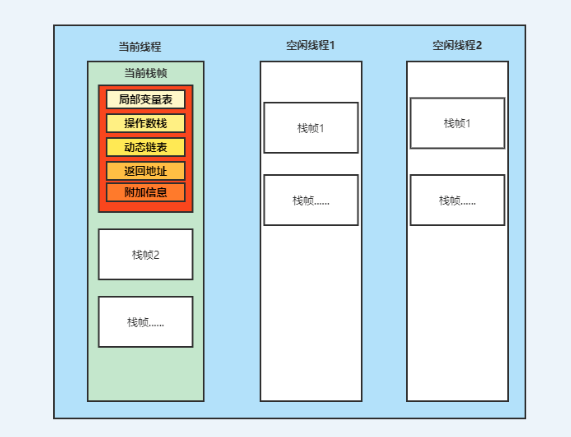
这里可以思考下，env其实就是一个查找表

每一个函数执行，就会有自己的env

     (define (square x)
       (* x x))
     
     (define (sum-of-squares x y) 
       (+ (square x) (square y))) 
     
     (define (f a)
       (sum-of-squares (+ a 1) (* a 2)))

用变动数据做模拟（Modeling with Mutable Data） #

可以看到，中文翻译其实对于理解还是有偏差的。感觉看英文理解可能更快一些。

mutable 这个单词，结合工作中的场景，确实是可以加速理解的。

这一章主要讲述了一些方法，可以更改之前说的 pair 就是套娃

(cons 1 
      (cons 2 
            (cons 3 
                  (cons 4 nil))))
(list 1 2 3 4)
'(1 2 3 4)

然后，可以实现一些复合的数据结构，比如队列（Quenes）、表格（Tables）

这一章中，还介绍了一种电路模拟语言，常见的与门非门等

通过一点点的编码，可以逐步的实现较为简单的电路

你可能想问，搞这么多有什么意义？
我也不知道，得等我仔细看完才知道有什么意义。

并发 #

讲述了并发问题，模拟了并发问题、死锁等

并且讲述了解决并发问题的手段

信号量（mutex）
scheme的串行化执行

流（Steams） #

介绍了概念，可以用Steam解决的复杂问题，比如可以用delay、force 等手段，将部分计算延迟执行，来提高执行效率

第四章：元语言抽象（Metalinguistic Abstraction） #

这一章主要围绕 eval 函数的实现进行讲解，并且可以在这个 eval 中实现各种比较有意思的计算

通过 eval apply 两个函数，实现代码的解析。

eval 函数的伪代码

(define (eval exp env)
(cond ((self-evaluating? exp) exp) 
  ((variable? exp) (lookup-variable-value exp env)) 
  ((quoted? exp) (text-of-quotation exp)) 
  ((assignment? exp) (eval-assignment exp env)) 
  ((definition? exp) (eval-definition exp env)) 
  ((if? exp) (eval-if exp env)) 
  ((lambda? exp) (make-procedure 
                  (lambda-parameters exp) 
                  (lambda-body exp) env))
  ((begin? exp) (eval-sequence (begin-actions exp) env)) 
  ((cond? exp) (eval (cond->if exp) env)) 
  ((application? exp) 
   (apply (eval (operator exp) env) 
          (list-of-values (operands exp) env))) 
  (else 
   (error 
    "Unknown expression type: EVAL" exp))))

apply 函数的实现

(define (apply procedure arguments)
	(cond ((primitive-procedure? procedure) 
         (apply-primitive-procedure procedure arguments))
        ((compound-procedure? procedure) 
         (eval-sequence (procedure-body procedure) 
                        (extend-environment 
                         (procedure-parameters procedure) 
                         arguments 
                         (procedure-environment procedure)))) 
    (else 
     (error 
      "Unknown procedure type: APPLY" procedure))))

比如你可以这么用这个eval函数

(eval '(define (factorial n)
         (if (= n 1) 1 (* (factorial (- n 1)) n))))

元循环求值器：这里将想办法实现一个 eval 函数，这个函数，可以执行一段内容，并且将内容的结果返回
scheme的变形——惰性求值：讨论的是应用序和正则序的区别
scheme的变形——非确定性计算：让scheme支持 nondeterminism 计算，比如看谁说谎了的问题
逻辑编程，一个粗略的解释

第五章：寄存器机器里的计算 #

这一章主要讲述的是如何将高级语言翻译成一种普遍的执行方式，揭开计算机程序的神秘面纱。

章节的序言，是开普勒的一句话：

My aim is to show that the heavenly machine is not a kind of divine, live being, but a kind of clockwork (and he who believes that a clock has soul atributes the maker’s glory to the work), insofar as nearly all the manifold motions are caused by a most simple and material force, just as all motions of the clock are caused by a single weight.
—Johannes Kepler (leter to Herwart von Hohenburg, 1605)

[!TIP]
老张叨叨叨
开普勒是著名的天文学家，所谓的 heavenly machine 应该指的是天体运行，这段话在我看来，应该是将天体运行唯物化的想法。
他用精密的钟表仪器类比天体，钟表看似神秘，运行精确，但是底层其实是通过简单的发票实现推动的。天体也类似。
作者在这里引用这段话，可能是想把【计算机】本身的进行反神秘化的说明，意在告诉大家，本章就会告诉大家，计算机是怎么实现的。

In this chapter we will describe processes in terms of the step-by-step operation of a traditional computer.
Such a computer, or register machine, sequentially executes instructions that manipulate the contents of a ﬁxed set of storage elements called registers.

寄存器机器的设计：介绍寄存器（Register Machines）的定义，并且通过scheme 实现一种通用寄存器，可以执行上面的各种程序

对比一下java中的设计：

这是一段java语言代码

public class Test {


    private static int add(int c){
        return c + 10;
    }


    public static void main(String[] args) {
        int a, b, c;
        a = 1;
        b = 2;
        c = add(a*b);
        c = c*(a+b);
    }

}

这个是javap -v 反编译后的字节码

Classfile /E:/Code/JAVA/JUC/out/production/JUC/net/ziruo/juc/Test.class
  Last modified 2019-10-29; size 546 bytes
  MD5 checksum 3526f85e07771be800502f7e10b50a3a
  Compiled from "Test.java"
public class net.ziruo.juc.Test
  minor version: 0
  major version: 52
  flags: ACC_PUBLIC, ACC_SUPER
Constant pool:
   #1 = Methodref          #4.#24         // java/lang/Object."<init>":()V
   #2 = Methodref          #3.#25         // net/ziruo/juc/Test.add:(I)I
   #3 = Class              #26            // net/ziruo/juc/Test
   #4 = Class              #27            // java/lang/Object
   #5 = Utf8               <init>
   #6 = Utf8               ()V
   #7 = Utf8               Code
   #8 = Utf8               LineNumberTable
   #9 = Utf8               LocalVariableTable
  #10 = Utf8               this
  #11 = Utf8               Lnet/ziruo/juc/Test;
  #12 = Utf8               add
  #13 = Utf8               (I)I
  #14 = Utf8               c
  #15 = Utf8               I
  #16 = Utf8               main
  #17 = Utf8               ([Ljava/lang/String;)V
  #18 = Utf8               args
  #19 = Utf8               [Ljava/lang/String;
  #20 = Utf8               a
  #21 = Utf8               b
  #22 = Utf8               SourceFile
  #23 = Utf8               Test.java
  #24 = NameAndType        #5:#6          // "<init>":()V
  #25 = NameAndType        #12:#13        // add:(I)I
  #26 = Utf8               net/ziruo/juc/Test
  #27 = Utf8               java/lang/Object
{
  public net.ziruo.juc.Test();
    descriptor: ()V
    flags: ACC_PUBLIC
    Code:
      stack=1, locals=1, args_size=1
         0: aload_0
         1: invokespecial #1                  // Method java/lang/Object."<init>":()V
         4: return
      LineNumberTable:
        line 8: 0
      LocalVariableTable:
        Start  Length  Slot  Name   Signature
            0       5     0  this   Lnet/ziruo/juc/Test;

  private static int add(int);
    descriptor: (I)I
    flags: ACC_PRIVATE, ACC_STATIC
    Code:
      stack=2, locals=1, args_size=1
         0: iload_0
         1: bipush        10
         3: iadd
         4: ireturn
      LineNumberTable:
        line 12: 0
      LocalVariableTable:
        Start  Length  Slot  Name   Signature
            0       5     0     c   I

  public static void main(java.lang.String[]);
    descriptor: ([Ljava/lang/String;)V
    flags: ACC_PUBLIC, ACC_STATIC
    Code:
      stack=3, locals=4, args_size=1
         0: iconst_1
         1: istore_1
         2: iconst_2
         3: istore_2
         4: iload_1
         5: iload_2
         6: imul
         7: invokestatic  #2                  // Method add:(I)I
        10: istore_3
        11: iload_3
        12: iload_1
        13: iload_2
        14: iadd
        15: imul
        16: istore_3
        17: return
      LineNumberTable:
        line 18: 0
        line 19: 2
        line 20: 4
        line 21: 11
        line 22: 17
      LocalVariableTable:
        Start  Length  Slot  Name   Signature
            0      18     0  args   [Ljava/lang/String;
            2      16     1     a   I
            4      14     2     b   I
           11       7     3     c   I
}

作者：那年十月
链接：https://juejin.cn/post/6844903983400632327
来源：稀土掘金
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

寄存器机器模拟器：上一章介绍了将普通程序翻译成 寄存器 程序的方式，这一章介绍一种验证逻辑的方案，判定翻译的是不是对了，其实就是单元测试。

存储分配和垃圾回收：通过编写 reg-evaluator，使用了list作为存储模型，但是list每次用完必须要回收，否则就会把内存用光，这里考虑如何实现垃圾回收

显示控制的求值器（The Explicit-Control Evaluator）：经过上面的寄存器形式的代码编译，最终可以实现一个可以执行 scheme 语言的计算器，这个计算的逻辑放到硬件中，就变成了这个芯片。

编译（Compilation）：将普通的scheme语言，变换成寄存器类型的语言

“Recursive Functions of Symbolic Expressions and Their Computation By Machine” （符号表达式的递归函数及其机械计算，McCarthy 1960） ↩︎