第一天的学习,会从基本开始,了解程序的基本概念,了解lisp语言,掌握基本代码的编写
计算过程的定义 #
计算过程是思维的高级抽象,看不见摸不着,但是又有现实的意义,可以完成某些智力的工作。
Figure 1: sora
程序就是这样无声无息的改变世界的。
一个计算过程需要精密而准确的执行相应的程序。
好的程序应该像是设计良好的汽车,或者是核反应堆一样,具有某种模块化的设计,其中的各个部分可以独立的构造、替换、排除错误。
用Lisp编程 #
lisp是20世纪50年代后期发明的一种语言,主要是为了对 list 进行 processing的语言。 称为【递归方程】,作者是John McCarthy2
是的,这里的lisp,其实就是 list + processing
Lisp的名字,来自表处理(LISt PROCESSING),Lisp语言的设计是提供了符号计算的能力,去解决一些程序设计问题 比如代数表达式的符号微分和积分。
Lisp不是刻意设计的结果,是一种实验性的,非正式的发展实现。lisp发展到现在,已经有很多种方言了,参见下面的发展图
![Figure 2: lisp的发展历程(from wikipedia)]](http://img.skydrift.cn/1708328694.png)
Figure 2: lisp的发展历程(from wikipedia)]
值得一说的是,ChezScheme3是业界最快的scheme编译器,之前是在思科的收费软件,后来进行了开源
lisp 主要的特点,在于将『数据』和『程序』进行了几乎无差别的对待,在数据处理方面,效果更好。
程序设计的基本元素 #
任何一门强力的程序设计语言,都需要考虑以下的一些概念
- 基本的表达形式 : 语言最基本的颗粒度
- 组合的方法 : 通过组合的方式,可以将简单的东西拼装成复杂的东西
- 抽象的方法 : 为复杂或者简单的东西命名,并将这些东西当做单元去操作
简明扼要,这其实就是语言的概念,少一个都不行。因此,在lisp中,其实只有5个元素
Expressions 表达式 #
学习语言最好的方式,就是有一个运行环境,在命令行里面敲代码,一边敲代码,一边执行。
个人理解,这里的命令行是指REPL(Read eval print loop),比如典型的,命令行就是一种REPL。 当然,大一些的函数,还是不方便在REPL中编写和运行的。但是一些小的,3-5行的还是比较合适。 pycharm就带一个python的REPL环境,如下图
Figure 3: python Console(REPL)
这里演示一些基本的lisp例子
(+ 137 349)
;486
在lisp中,计算逻辑使用了前缀表达式(prefix-notation) 前缀表达式虽然反直觉,但是有很多优点
- 随意扩充
(* 1 2 3 4 5) - 随意嵌套
(* (+ 1 2) (- 2 1))
但是也有一些缺点,比如不格式化的化,很难看明白
Naming and the Environment 命名和环境 #
命名 :将一段代码,通过 define 关键字,创建别名,可以随意引用
环境 :环境是程序运行中的内存,会存储已经命名过的名字+名字代表的对象(pair)
(define size 2)
(* 2 size)
Evaluation Combinations 组合式求值 #
一种分而治之的思想,整体程序的运行,其实就是两步
- 分开求所有子表达式(sub-expressions)的值(operands)
- 将所有表达式的值(the operands)使用操作符(the operator)进行计算
求值的过程,就称之为 conbination
可以照着这张图进行理解
(* (+ 2 (* 4 6))
(+ 3 5 7))
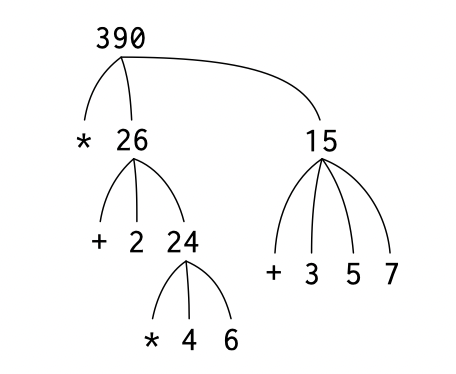
Figure 4: 表达式求值示意图(来源原书)
你会发现,这些符号中, + 这种的属于内置符号(built-in),
你自己定义的 size 这种的属于命名符号,
但是对于 (define x 2) 这种的表达式,lisp采取的措施就不是求值,
这属于特殊的规则(special form)
Compound Procedures 复合过程 #
lisp中的元素到现在,总体介绍分为以下的
- 数字、算数,作为基础数据和过程
- 可嵌套的组合,提供了一种组合的手段
- 定义,将name和values关联在一起,提供了抽象
本章节, 将会介绍更强力的工具:过程定义(procedure definitions),可以针对一个元素进行抽象重命名
这不就是函数me
(define (square x) (* x x))
;基本的定义语句如下:
(define (⟨name⟩ ⟨formal parameters⟩)
⟨ body⟩)
(define (sum-of-squares x y)
(+ (square x) (square y)))
(define (f a)
(sum-of-squares (+ a 1) (* a 2)))
光看过程,其实无法猜测里面是什么东西
The Substitution Model for Procedure Application 过程的代换模型 #
代换模型(substitution model)简言之,就是在过程执行的时候, 系统会将抽象的名字换成原始的过程,并且运行。
说白了,其实就遍历二叉树,深度遍历二叉树。 递归,将所有表达式入栈, 递归到最末尾,依次求值出栈。
当然,现实中的编译器、解释器不只是代换这么简单,还会更加复杂。 书籍的 第五章 会给出一个完整的解释器和编译器。
是否有点期待呢? 现在看了目录之后,发现总共就只有5章,突然有点慌
Applicative order versus normal order 应用序 和正则序 #
比如计算下面的表达式
(f 5)
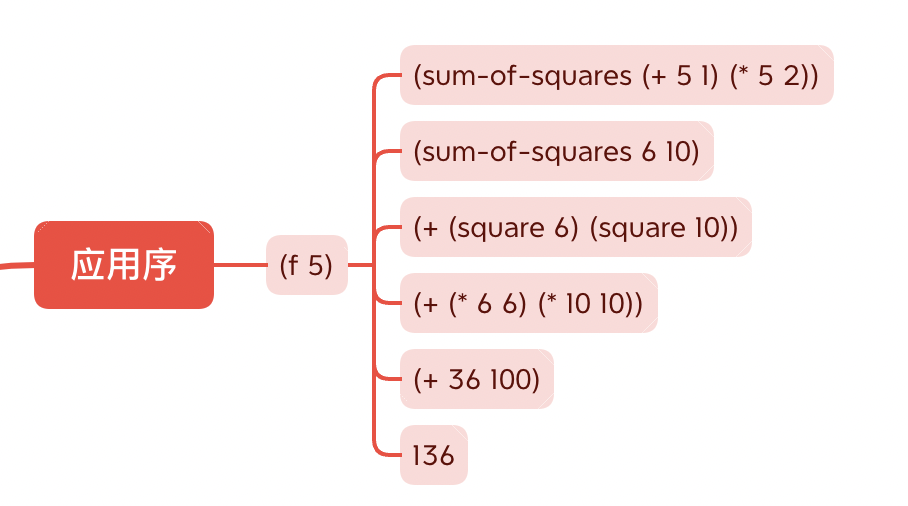
Figure 5: 应用序
应用序(Applicative order),是计算的过程中能算就算,当然是基础计算 缺点是不直观,优点是速度较快,scheme中,用的就是应用序的代换模型

Figure 6: 正则序
正则序(normal order),则是代换的过程中绝不计算,都代换完在计算
优点是直观,缺点则是部分需要重复计算,比如这里的 (+ 5 1)
“fully expand and then reduce”
在某些练习中,正则序和应用序表现的效果也不一样的。
; Exercise 1.5
(define (p) (p))
(define (test x y)
(if (= x 0) 0 y))
; (test 0 (p)) 直接死循环了
;; 这里用了app order的话,会先对param求值,(p)本身就是死循环
;; 如果用了正则序,则不会求值,会一直expend,(p)不会被执行,则返回0
;; https://www.cnblogs.com/ssaylo/p/13633403.html
Conditional Expressions and Predicates #
这是介绍第二个 special form 就是控制流:if
(define (abs x)
(cond ((> x 0) x)
((= x 0) 0)
((< x 0) (- x))
)
)
上面这个例子,就是基本的if语句
通过cond这个关键字,进行 「case analysis」 这个动作, cond 的标准用法如下,可以包含多个条件和执行内容
其中,p 代表 predicate,需要返回true 或者 false,e 代表执行的表达式
从p1 开始执行,如果true,则执行,如果fase,就执行下一个。如果都为false,则返回 undifined
(cond (⟨p1 ⟩ ⟨e1 ⟩)
(⟨p2 ⟩ ⟨e2 ⟩)
...
(⟨pn ⟩ ⟨en ⟩))
控制流的cond,还会有一个默认的选项
(define (abs x)
(cond ((< x 0) (- x))
(else x)))
另外,scheme中还提供了原生的 if 关键字,这里更像一个三目运算符
(define (abs x)
(if (< x 0)
(- x) x))
predicate 也支持进行组合
- and
(and ⟨e 1⟩ . . . ⟨e n⟩) - or
(or ⟨e 1⟩ . . . ⟨e n⟩) - not
(not ⟨e⟩)
比如,你可以自己亲手定义 >=
(define (>= x y) (or (> x y) (= x y)))
;or
(define (>= x y) (not (< x y)))
cond 也支持对操作符进行设置,如下:
(define (a-plus-abs-b a b)
((if (> b 0) + -) a b))
openAI在24年2月推出的文生视频模型 sora https://openai.com/sora ↩︎
“Recursive Functions of Symbolic Expressions and Their Computation By Machine” (符号表达式的递归函数及其机械计算,McCarthy 1960) ↩︎
思科官方的chezScheme 用户手册 https://cisco.github.io/ChezScheme/csug9.5/index.html ↩︎

