通过已经学习到的东西，矫正概念，进行更有意思的计算

Day 1 的复习 #

通过了第一天的学习，基本上明白了以下的内容

1. 程序的结构，基础元素等
2. lisp语言的基础
   1. 基本元素计算，前缀表达式， prefix-notation
   2. special forms 特殊元素， define, cond
   3. 由于1、2组合而成的复合表达式
   4. 针对符合表达式，通过 代换模型 subsitution model 进行人工智能的计算（笑）
3. 做了一些练习题
   1. 在lisp中，操作符也可以用来 cond
   2. 人工智能代换的时候，有2种顺序，应用序和正则序，两者在极端场景下，效果不一样

数学概念和计算机概念的区分 #

数学比较重要的是概念定义，严谨的定义；计算机概念中，更重视的是操作。 书中举例说了，比如要计算平方根 数学概念很简单

x 的平方根 = the y such that y ≥ 0 and y 的平方 = x.

但是这只是个概念，无法用来计算，写一样的lisp代码也没办法计算。

可操作的平方根计算 #

比较通常的办法，就是使用牛顿的逐步逼近法（successive approximations）

我看到这里开始一脸懵逼了

1. 平方根的逼近求值法 ¹
2. 迭代法求平方根 ²
3. quara的一个比较好的回答 ³

参考了一个文档，逐渐明白一些了，

牛顿法求平方根的数学理解 #

牛顿法的具体推导过程

$y = x^2$ 这个函数，坐标系中，是经典的反抛物线图案，求 根号2 的时候，相当于y=2，求x的值。 结合图像分析，相当于是求 纵坐标 y=2的时候，曲线对应x的横坐标。

牛顿法的话，结合右图进行分析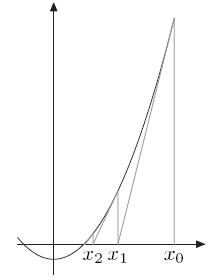

1. 将 $y = x^2,y=2$ 进行简化，变成 $0= x^2 - 2$，就变成了上图的样子
2. 这样一来，曲线和x轴的交点就变成了要求的根号2，整个函数变成了 $f(x) = x^2 -2$
3. 随便找一个 $x_0$ 点，针对 $x_0$ 进行求导，$f’(x) = 2x$，如图，导数是一条直线
4. 直线与$x$ 轴的交点，作为 $x_1$ ，可以明显看到，$x_1$ 会更接近实际的 $x$，但是不等于 $x$
5. 继续3的步骤，直到 $x_n$，会逐步收敛到 $x$，进而求出非常接近的 $x$

以上，就是结合图形的直观理解，可以看到，这个方法非常的直观

接下来，会结合上面的直观理念，进行公式级别的推导计算

看下上面的图，已知条件如下

1. 直线的斜率为 $f’(x_0)$
2. 直线经过了一个点：$(x_0, f(x_0))$ ，这就是在曲线找到的一个随机点
3. 直线经过了另一个点：$(x_1, 0)$，这就是x轴的交点

可以得到2个公式

$基础公式：y = f’(x_0)x_1 + b , 其中, 斜率为 f’(x_0)$

套用2个点位，可以得到下面2个公式,

1. 套用 $(x_0, f(x_0)) : f(x_0) = f’(x_0)x_0+b$
2. 套用 $(x_1, 0) : 0 = f’(x_0)x_1+b$

两个公式进行相减，可以将b消除，并且得到可以便于计算的公式

$f(x_0) = f’(x_0)x_0 - f’(x_0)x_1$

公式进行变换，则可以得到对于 \(x_1\) 的求值公式

至此，求值公式已经ok，对于一元二次方程，展开的方式⁴已经非常明显了。

将公式套用到 $f(x) = x^2-2$ 的话，从 $x_0$ 计算 $x_1$ 的方式就很简单了

经过简化，公式如下

使用scheme实现牛顿法 #

实现代码很简单

(define (sqrt x)
  (sqrt-iter 1.0 x))

主入口函数，就是sqrt这个，其中调用了 sqrt-iter 这个函数，这个函数有2个入参 1.0 就是初始的 $x_0$ x 则是要求的目标值

(define (sqrt-iter guess x)
 (if (good-enough? guess x)
     guess
     (sqrt-iter (improve guess x) x)))

sqrt-iter 函数的定义如上 这个函数内部其实就只有一个判定 如果收敛到目标值，就返回，否则，优化并且迭代

(define (improve guess x)
  (average guess (/ x guess)))

(define (average x y)
  (/ (+ x y) 2))
(define (good-enough? guess x)
  (< (abs (- (square guess) x)) 0.001))

其中的3个子函数如上。都比较简单

good-enough? 用来判定是否达到了收敛阈值，可以看到，判定是相对反向的： 通过 square 方法，来判定计算的value进行平方以后和目标值的差距。

average 中规中矩的函数，求平均数

improve 这是核心函数，用来计算新的 $x_n$, guess 就是 $x_{n-1}$，$x$ 就是 $y$

这个函数整体就是在执行公式5，即 $x_1=\frac{x_0+\frac{2}{x_0}}{2}$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

  (define (square x)
    (* x x))

  (define (sqrt-iter guess x)
    (if (good-enough? guess x)
      guess
      (sqrt-iter (improve guess x) x)))

  (define (improve guess x)
    (average guess (/ x guess)))

  (define (average x y)
    (/ (+ x y) 2))
  (define (good-enough? guess x)
    (< (abs (- (square guess) x)) 0.001))


  (define (sqrt x)
    (sqrt-iter 1.0 x)
)

版本1 的代码如上。

可以看到，这其中是有一段递归的，比如 sqrt-iter 调用了自己，可以将上面的函数调用关系， 变成一棵树展示出来

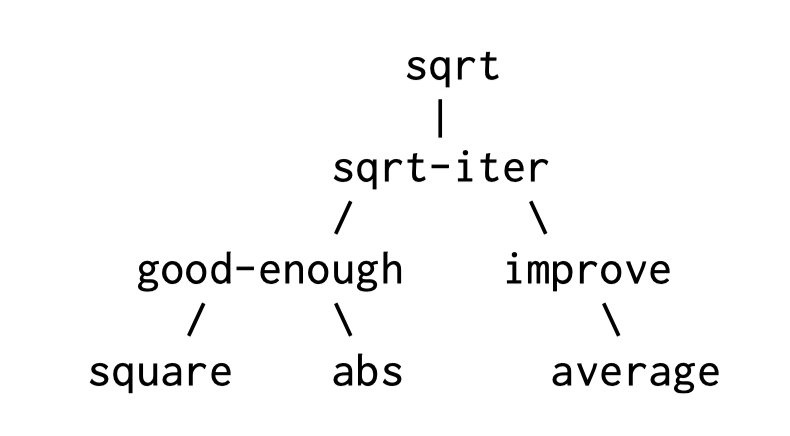
函数被拆解成了不同的小结构，每个结构各司其职，都封装了逻辑， 每个小结构逻辑都很简单。

每个大结构，不会也不需要关注小结构的内部实现。这就是抽象层次的问题。 大的结构，抽象层次高，小结构抽象层次低，

抽象层次也只是层次，不代表复杂度，抽象层次高的函数，不一定就会比低层次的更复杂。

块封装 和 局部变量控制 #

可以看到，在这个过程中，很多函数名称出现了

(define (sqrt x)

  (define (good-enough? guess x)
    (< (abs (- (square guess) x)) 0.001))
  (define (improve guess x) (average guess (/ x guess)))

  (define (sqrt-iter guess x)
     (if (good-enough? guess x)
         guess
         (sqrt-iter (improve guess x) x)))
(sqrt-iter 1.0 x)
)

如上，这是第二版改动，可以看到，把一些工具函数，可以直接定义在大函数内部，这样，就算是一个更高级别的封装了

不会污染全局变量，内部定义的函数，可见性只限制在内部

进一步的说明，变量 x 也是一个局部变量，可以共享使用

(define (sqrt x)

 (define (good-enough? guess)
  (< (abs (- (square guess) x)) 0.001))

 (define (improve guess)
   (average guess (/ x guess)))

 (define (sqrt-iter guess)
  (if (good-enough? guess)
      guess
      (sqrt-iter (improve guess))))
(sqrt-iter 1.0)
)

这种情况，称之为 词法作用域 (lexical scoping)

在现代的编程中，这种块结构稀松平常，比如

1. 面向对象编程
2. 重构改善
3. 设计模式
4. 领域对象模型等

这些讨论的，其实都是如何用好这种 块结构 ，却很少有人讨论这种结构一开始是怎么设计出来的，来源于 老的 Algol 60 语言。

过程和计算 #

编写程序也是有各种套路的，就像是摄影和下棋一样，学会了套路和流程，才算是上道儿了。 接下来，就要介绍各种组合拳了。

1. 研究各种函数流程的执行结构
2. 研究不同执行流程的时间复杂度，空间复杂度
3. 这些代表性的函数，只是用来演示的，不能作为生产环境使用

迭代 VS 递归 #

不知道大家是怎么看待 这两个概念的，其实我本身在阅读之前，是没有明确的区别的。

由于之前学了yin神的计算机课，大概知道了迭代是递归的一种（尾递归），但是还是看出了解一下比较好

阶乘的实现举例 递归实现：

(define (factorial n)
   (if (= n 1)
       1
       (* n (factorial (- n 1)))))

迭代实现：

(define (factorial n)
  (fact-iter 1 1 n))

(define (fact-iter product counter max-count)
  (if (> counter max-count)
      product
     (fact-iter (* counter product) (+ counter 1) max-count)))

可以看到，递归在执行的时候，其实是 不计算 的，只有都展开之后才开始计算；而迭代则不一样，每次迭代都会计算。

递归 ：就递归来说，递归有明显的展开和收缩的过程，这个过程产生一种链条（chain），每次调用都有一种延迟计算（deferred operations）挂靠在链条上。 解释器要执行递归，需要把chain都保存起来，这个例子中，空间的增长是线性的(n 的正比)，这就是一个 线性递归 的过程

迭代 ：这个过程中，没有展开和收缩的过程，每次执行，就是单独的，这种过程就是一个 迭代计算 过程

注意，代码中有递归调用，并不代表这个计算过程是递归的，比如 迭代实现中，也有 fact-iter 的递归调用

这就是 递归计算过程 和 递归函数 的区别。

一个简单的可以看出来到底是递归还是迭代的办法，就是看下递归的表达式 看下这个表达式，是否会阻碍了其他表达式的计算⁵

比如

 (define (++ a b)
   (if ( = a 0)
       b
       (inc (++ (dec a) b))) ;; 最后的求值表达式中，有inc在++外面，导致inc进行了延迟计算，这样就产生了chain
   )

;; (++ 4 5)
;; (inc (++ 3 5)))
;; (inc (inc (++ 2 5)))
;; (inc (inc (inc (++ 1 5))))
;; (inc (inc (inc (inc (++ 0 5)))))
;; (inc (inc (inc (inc (5)))))
;; (inc (inc (inc (6))))
;; (inc (inc 7))
;; (inc 8)
;; 9

  (define (++ a b)
   (if ( = a 0)
   b
   (++ (dec a) (inc b)))) ;; 最后的求值表达式中，inc 在++里面
;;(++ 4 5)
;;(++ 3 6)
;;(++ 2 7)
;;(++ 1 8)
;;(++ 0 9)
;;9