SICP 练习1-14 #
题目 #
Draw the tree illustrating the process generated by the count-change procedure of Section 1.2.2 in making change for 11 cents. What are the orders of growth of the space and number of steps used by this process as the amount to be changed increases?
使用『找零钱』算法，用5枚硬币找出来11美分，即$f(11,5)$，绘制这个算法的过程，并且思考在这个算法中，对于空间复杂度和时间复杂度的计算方式。
(define (change amount coins)
(-> exact-integer? (listof exact-integer?) exact-integer?)
(define (cc amount kind-of-coins)
(cond [(= amount 0) 1]
[(or (< amount 0) (= kind-of-coins 0)) 0]
[else (+
(cc amount (- kind-of-coins 1))
(cc (- amount (list-ref coins (- kind-of-coins 1))) kind-of-coins)
)
]
))
(cc amount (length coins))
)
;; 使用方式
(change 11 '(1 2 5 10 50))
转载 & 学习 #
https://sicp-solutions.net/post/sicp-solution-exercise-1-14/
这是一篇非常棒的分析，本文全依托于这篇文章进行分析和学习
人工智能代换理解 #
图形化1：脑图 #
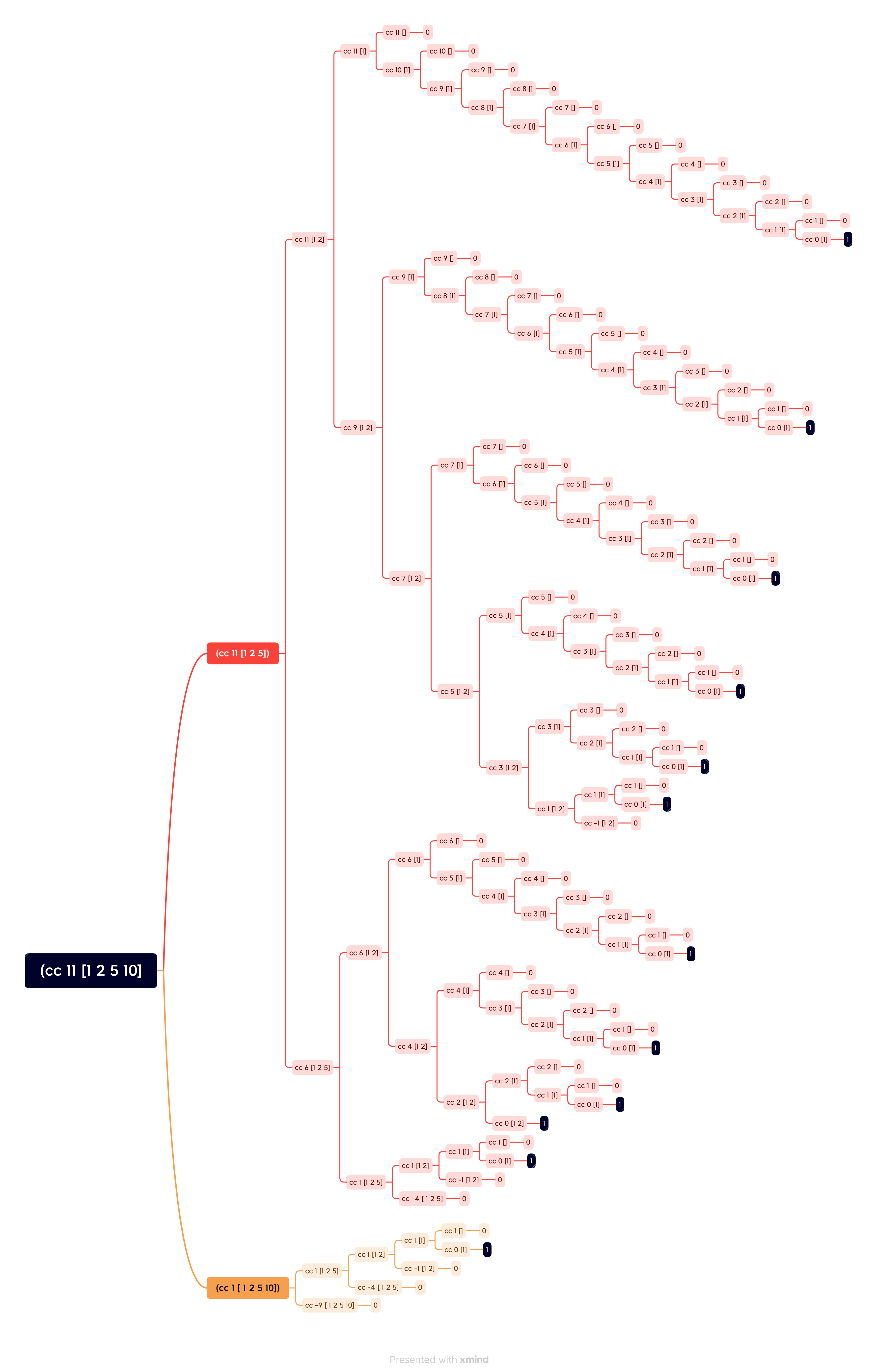可以看到上面的图，计算逻辑全部都代换出来的话，是非常长的，大约有 220行（每行是一个计算节点)
图形化2：剪枝 #
如果将重复的节点进行剪枝的话，可以节省很多的空间
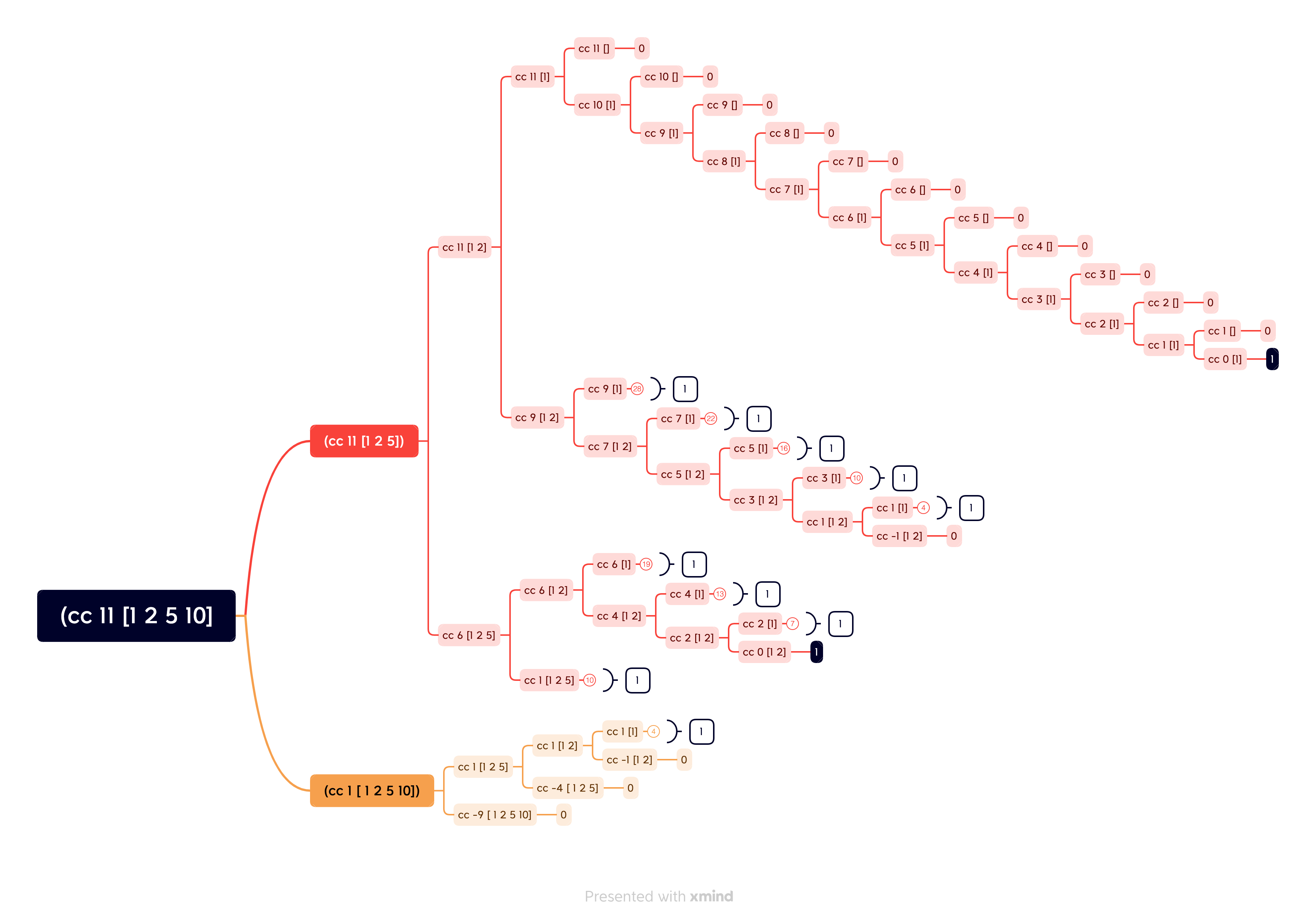
可以看到，通过这样的方式进行剪枝，可以极大的节省计算逻辑
图形化3：graphviz #
用脑图表现还是不太完美，可以这个库graphviz来表现，效果更好，有在线渲染库
graphviz web sandbox editors like graphviz visual editor and Graphviz Online
将下面的文本粘贴，则得到一张好看的图
digraph G {
node [color = gray95,style=filled];
graph [ranksep=0.25];
node [color = gray95,style=filled,fontsize=9,shape=box, margin=.08, width=0, height=0 ];
edge [penwidth=.5, arrowsize=0.5];
"[0] (cc 11 5)" [label="(cc 11 5)", ];
"[0] (cc 11 5)" -> "[1] (cc 11 4)"; "[1] (cc 11 4)" [label="(cc 11 4)", ];
"[1] (cc 11 4)" -> "[2] (cc 11 3)"; "[2] (cc 11 3)" [label="(cc 11 3)", ];
"[2] (cc 11 3)" -> "[3] (cc 11 2)"; "[3] (cc 11 2)" [label="(cc 11 2)", ];
"[3] (cc 11 2)" -> "[4] (cc 11 1)"; "[4] (cc 11 1)" [label="(cc 11 1)", ];
"[4] (cc 11 1)" -> "[5] (cc 11 0)"; "[5] (cc 11 0)" [label="(cc 11 0)", ];
"[4] (cc 11 1)" -> "[5] (cc 10 1)"; "[5] (cc 10 1)" [label="(cc 10 1)", ];
"[5] (cc 10 1)" -> "[6] (cc 10 0)"; "[6] (cc 10 0)" [label="(cc 10 0)", ];
"[5] (cc 10 1)" -> "[6] (cc 9 1)"; "[6] (cc 9 1)" [label="(cc 9 1)", ];
"[6] (cc 9 1)" -> "[7] (cc 9 0)"; "[7] (cc 9 0)" [label="(cc 9 0)", ];
"[6] (cc 9 1)" -> "[7] (cc 8 1)"; "[7] (cc 8 1)" [label="(cc 8 1)", ];
"[7] (cc 8 1)" -> "[8] (cc 8 0)"; "[8] (cc 8 0)" [label="(cc 8 0)", ];
"[7] (cc 8 1)" -> "[8] (cc 7 1)"; "[8] (cc 7 1)" [label="(cc 7 1)", ];
"[8] (cc 7 1)" -> "[9] (cc 7 0)"; "[9] (cc 7 0)" [label="(cc 7 0)", ];
"[8] (cc 7 1)" -> "[9] (cc 6 1)"; "[9] (cc 6 1)" [label="(cc 6 1)", ];
"[9] (cc 6 1)" -> "[10] (cc 6 0)"; "[10] (cc 6 0)" [label="(cc 6 0)", ];
"[9] (cc 6 1)" -> "[10] (cc 5 1)"; "[10] (cc 5 1)" [label="(cc 5 1)", ];
"[10] (cc 5 1)" -> "[11] (cc 5 0)"; "[11] (cc 5 0)" [label="(cc 5 0)", ];
"[10] (cc 5 1)" -> "[11] (cc 4 1)"; "[11] (cc 4 1)" [label="(cc 4 1)", ];
"[11] (cc 4 1)" -> "[12] (cc 4 0)"; "[12] (cc 4 0)" [label="(cc 4 0)", ];
"[11] (cc 4 1)" -> "[12] (cc 3 1)"; "[12] (cc 3 1)" [label="(cc 3 1)", ];
"[12] (cc 3 1)" -> "[13] (cc 3 0)"; "[13] (cc 3 0)" [label="(cc 3 0)", ];
"[12] (cc 3 1)" -> "[13] (cc 2 1)"; "[13] (cc 2 1)" [label="(cc 2 1)", ];
"[13] (cc 2 1)" -> "[14] (cc 2 0)"; "[14] (cc 2 0)" [label="(cc 2 0)", ];
"[13] (cc 2 1)" -> "[14] (cc 1 1)"; "[14] (cc 1 1)" [label="(cc 1 1)", ];
"[14] (cc 1 1)" -> "[15] (cc 1 0)"; "[15] (cc 1 0)" [label="(cc 1 0)", ];
"[14] (cc 1 1)" -> "[15] (cc 0 1)"; "[15] (cc 0 1)" [label="(cc 0 1)",color=gray80];
"[3] (cc 11 2)" -> "[4] (cc 6 2)"; "[4] (cc 6 2)" [label="(cc 6 2)", ];
"[4] (cc 6 2)" -> "[5] (cc 6 1)"; "[5] (cc 6 1)" [label="(cc 6 1)", ];
"[5] (cc 6 1)" -> "[6] (cc 6 0)"; "[6] (cc 6 0)" [label="(cc 6 0)", ];
"[5] (cc 6 1)" -> "[6] (cc 5 1)"; "[6] (cc 5 1)" [label="(cc 5 1)", ];
"[6] (cc 5 1)" -> "[7] (cc 5 0)"; "[7] (cc 5 0)" [label="(cc 5 0)", ];
"[6] (cc 5 1)" -> "[7] (cc 4 1)"; "[7] (cc 4 1)" [label="(cc 4 1)", ];
"[7] (cc 4 1)" -> "[8] (cc 4 0)"; "[8] (cc 4 0)" [label="(cc 4 0)", ];
"[7] (cc 4 1)" -> "[8] (cc 3 1)"; "[8] (cc 3 1)" [label="(cc 3 1)", ];
"[8] (cc 3 1)" -> "[9] (cc 3 0)"; "[9] (cc 3 0)" [label="(cc 3 0)", ];
"[8] (cc 3 1)" -> "[9] (cc 2 1)"; "[9] (cc 2 1)" [label="(cc 2 1)", ];
"[9] (cc 2 1)" -> "[10] (cc 2 0)"; "[10] (cc 2 0)" [label="(cc 2 0)", ];
"[9] (cc 2 1)" -> "[10] (cc 1 1)"; "[10] (cc 1 1)" [label="(cc 1 1)", ];
"[10] (cc 1 1)" -> "[11] (cc 1 0)"; "[11] (cc 1 0)" [label="(cc 1 0)", ];
"[10] (cc 1 1)" -> "[11] (cc 0 1)"; "[11] (cc 0 1)" [label="(cc 0 1)",color=gray80];
"[4] (cc 6 2)" -> "[5] (cc 1 2)"; "[5] (cc 1 2)" [label="(cc 1 2)", ];
"[5] (cc 1 2)" -> "[6] (cc 1 1)"; "[6] (cc 1 1)" [label="(cc 1 1)", ];
"[6] (cc 1 1)" -> "[7] (cc 1 0)"; "[7] (cc 1 0)" [label="(cc 1 0)", ];
"[6] (cc 1 1)" -> "[7] (cc 0 1)"; "[7] (cc 0 1)" [label="(cc 0 1)",color=gray80];
"[5] (cc 1 2)" -> "[6] (cc -4 2)"; "[6] (cc -4 2)" [label="(cc -4 2)", ];
"[2] (cc 11 3)" -> "[3] (cc 1 3)"; "[3] (cc 1 3)" [label="(cc 1 3)", ];
"[3] (cc 1 3)" -> "[4] (cc 1 2)"; "[4] (cc 1 2)" [label="(cc 1 2)", ];
"[4] (cc 1 2)" -> "[5] (cc 1 1)"; "[5] (cc 1 1)" [label="(cc 1 1)", ];
"[5] (cc 1 1)" -> "[6] (cc 1 0)"; "[6] (cc 1 0)" [label="(cc 1 0)", ];
"[5] (cc 1 1)" -> "[6] (cc 0 1)"; "[6] (cc 0 1)" [label="(cc 0 1)",color=gray80];
"[4] (cc 1 2)" -> "[5] (cc -4 2)"; "[5] (cc -4 2)" [label="(cc -4 2)", ];
"[3] (cc 1 3)" -> "[4] (cc -9 3)"; "[4] (cc -9 3)" [label="(cc -9 3)", ];
"[1] (cc 11 4)" -> "[2] (cc -14 4)"; "[2] (cc -14 4)" [label="(cc -14 4)", ];
"[0] (cc 11 5)" -> "[1] (cc -39 5)"; "[1] (cc -39 5)" [label="(cc -39 5)", ];
}
时间复杂度计算 #
实在是不好算，但是也可以进行分解，并且一点点找到规律
$f(n,1)$的计算 #
看到这张图，应该比较明显了，可以看到，$f(n,1)$ 每个节点，都会分解为2个节点，并且加上一个最终节点
$$ T(n,1) = 2n+1 $$$f(n,2)$的计算 #
看到这张图，可以发现，$f(n,2)$ 的节点，会拆分成 x个 $f(n,1)$的节点，这里的x，大约和硬币的面额有关，就假如是个常数a，那么$x=n/a$，那么，整体的节点数量，就是下面的公式
$$ T(n,2) = \frac na +1 + (2n-1)*(\frac na+1)-2a\sum_{i=0}^{n/a}(i) $$ $$ T(n,2) = \frac{2n}a +1 + \frac{2n^2} {a}-\frac{n}{a}+2n-1-2a\sum_{i=0}^{n/a}(i) $$ $$ T(n,2) = \frac{n}a + \frac{2n^2}{a} + 2n - 2a\sum_{i=0}^{n/a}(i) $$求和公式已经全都忘记了，这里只能先暂停，然后继续推导求和公式了，有已经会的同学，自行跳走
为了简便计算，令a=2，n=11
$T(n,2) = 11/2 +1 + \sum_{i=0}^{11/2}(211-22i+1)$
$T(n,2) = 5 +1 + \sum_{i=0}^{5}(22-4i+1)$
$T(n,2) = 6 + \sum_{i=0}^{5}(21-4i)$
$T(11,2) = 6 + (21-40)+(21-41)+(21-42)+(21-43)+(21-44)+(21-45)$
$T(11,2) = 6+ 21*(5+1)-4*(0+1+2+3+4+5)$
$T(11,2) = 6+ 21*(5+1)-4\sum_{i=0}^5(i)$
$T(11,2) = (11/2 +1) + (211-1)(11/2+1)-4\sum_{i=0}^5(i)$
$T(n,2) = n/a +1 + (2n-1)*(n/a+1)-2a\sum_{i=0}^5(i)$
$$ T(n,2) = \frac{n}a + \frac{2n^2}{a} + 2n -2a\sum_{i=0}^{n/a}(i) \\ $$ $$ T(n,2) = \frac{n}a + \frac{2n^2}{a} + 2n-2a(\frac{(n/a)^2 + 2*(n/a)}{2}) \\ $$ $$ T(n,2) = \frac{n}a + \frac{2n^2}{a} + 2n -a(n/a)^2 - 2a*(n/a) \\ $$ $$ T(n,2) = \frac{n}a + \frac{2n^2}{a} + 2n -\frac{n^2}{a} - 2n \\ $$ $$ T(n,2) = \frac{n}a + \frac{n^2}{a} \\ $$不行了，这里需要继续推导等差数列的求和公式了
$\sum_{i=0}^5(i) = 0+1+2+3+4+5$
$\sum_{i=0}^5(i) = 15$
$\sum_{i=0}^5(i) = (\frac52+1)*5$
$\sum_{i=0}^n(i) = (\frac{n}{2}+1)*n$
$\sum_{i=0}^n(i) = \frac{n^2+2n}{2}$
即，时间复杂度是这样的
$$ T(n,2) =\mathrm\Theta(n^2) $$$f(n,3)$的计算 #
同理，对于$f(n,3)$ 则可以进行进一步的拆解
也是类似的分解，只是常数a不一样
$$ T(n,3)= \frac{n}{a}+1+\sum_{i=0}^{\frac{n}{a}}T(n-ai,2) \\ T(n,3) =\mathrm\Theta(n^3) $$$f(n,m)$的计算 #
最终的复杂度，则 $T(n,m)=\Theta(n^m)$
空间复杂度计算 #
递归的空间复杂度，主要就是递归的深度，可以看到，最深的地方在于$f(n,1)$，其他的部分，都是树形展开
由此可见，空间复杂度最多的部分，就是
$$ \Theta(n) $$